probability - Proof explanation - weak law of large numbers - Mathematics Stack Exchange

Let $(X_i)$ be i.i.d. random variables with mean $\mu$ and finite variance. Then $$\dfrac{X_1 + \dots + X_n}{n} \to \mu \text{ weakly }$$ I have the proof here: What I don't understand is, why it

How Did We Get Here? The Tangled History of the Second Law of Thermodynamics—Stephen Wolfram Writings

Proof of the Law of Large Numbers Part 2: The Strong Law, by Andrew Rothman

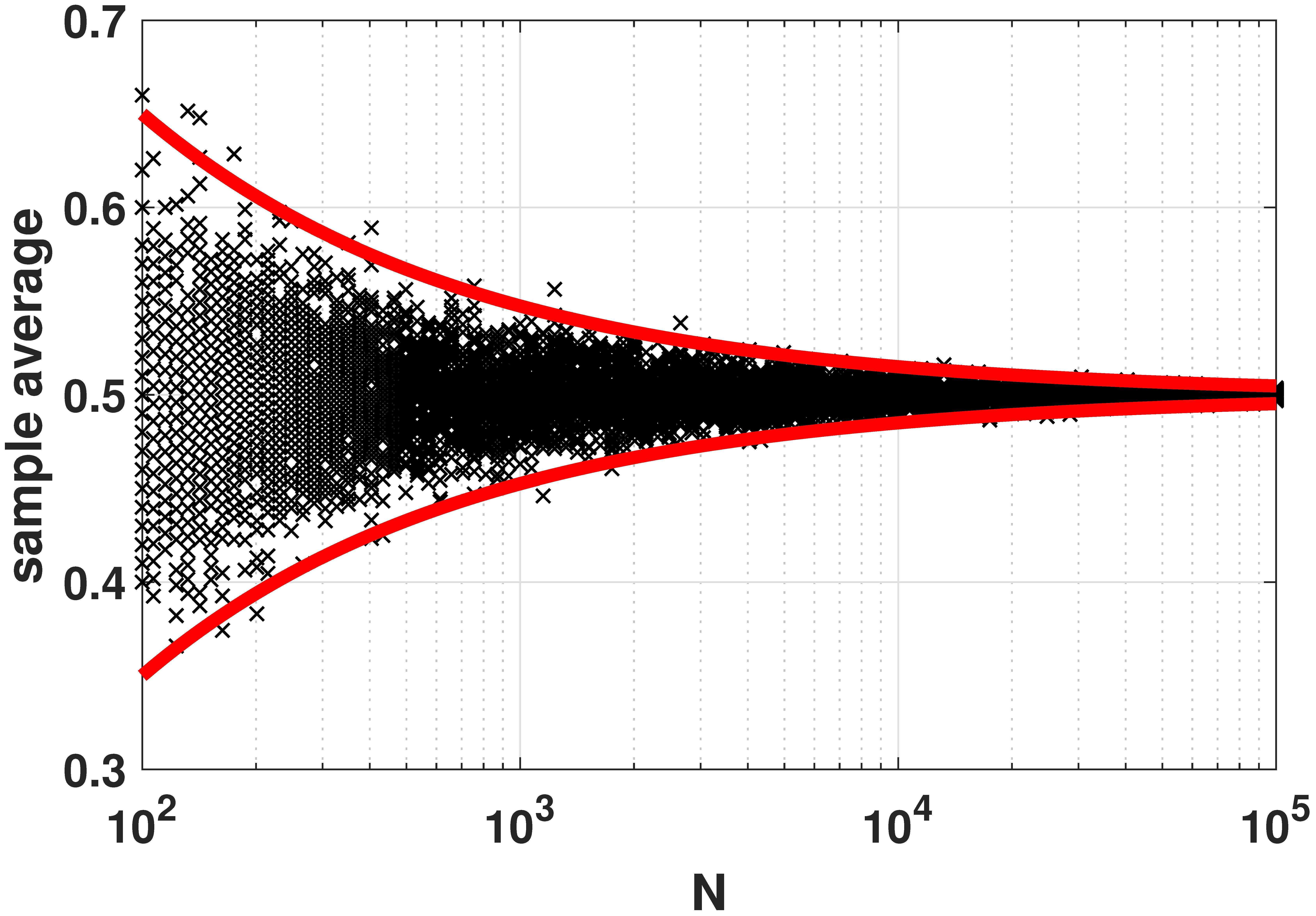
Week 121 Law of Large Numbers Toss a coin n times. Suppose X i 's are Bernoulli random variables with p = ½ and E(X i ) = ½. The proportion of

Proof of the Law of Large Numbers Part 2: The Strong Law, by Andrew Rothman

statistics - Expectation of square of random variable and their mean. - Mathematics Stack Exchange

Law of Large Numbers Strong and weak, with proofs and exercises

reference request - Famous examples of serendipity in 20th century mathematics - MathOverflow

probability theory - Strong Law of Large Numbers (Klenke's proof) - Mathematics Stack Exchange

econometrics - Is this use of a Law of Large Numbers correct? - Economics Stack Exchange

Law of Large Numbers: What It Is, How It's Used, Examples

L18.4 The Weak Law of Large Numbers

Winning Strategies - Law of Large Numbers in Gambling

Law of Large Numbers: What It Is, How It's Used, Examples

limits - Questions on Inverting Laplace transforms and Probability - Mathematics Stack Exchange

fourier analysis - Proving Weierstrass' Approximation Theorem - Mathematics Stack Exchange